In microeconomics, production functions and isoquant curves are essential for analyzing how firms combine inputs—like labor and capital—to produce goods and services efficiently. These tools offer critical insights into how businesses make decisions to maximize output while minimizing costs. They also help economists understand how production strategies respond to changing input levels and guide firms toward optimal input combinations.
This guide provides a detailed examination of production functions, including the Cobb-Douglas production function, the Law of Production, and isoquant curves.
What is a Production Function?
A production function expresses the relationship between the inputs used in production and the resulting output. It identifies how much output a firm can generate from different quantities of labor and capital, offering a roadmap for firms to allocate resources efficiently.
The general form of a production function is given by:
[ Q = f(L, K) ]
Where (Q) is the quantity of output produced, (L) is the quantity of labor, (K) is the quantity of capital, and (f) represents the functional relationship between inputs and outputs. This equation provides a roadmap for firms, guiding them in deciding how changing input levels affect their output and helping them determine optimal input mixes.
Types of Production Functions
The way inputs affect output varies across different industries and production processes. There are several key types of production functions that reflect these differences.
Linear Production Function
In a linear production function, the relationship between inputs and outputs is proportional. If a firm doubles its labor and capital, its output also doubles. Although useful in theoretical analysis, this model is often unrealistic because it assumes perfect substitutability between inputs.
[ Q = aL + bK ]
Leontief Production Function
The Leontief production function models industries where inputs are used in fixed proportions. It is appropriate for scenarios where inputs must be combined in specific ratios, such as assembly-line manufacturing. In this case, increasing one input alone will not increase output, as production is limited by the scarcest resource.
[ Q = min(aL, bK) ]
Cobb-Douglas Production Function
The Cobb-Douglas production function is widely used in economic analysis because it allows for diminishing returns and varying levels of input substitutability.
[ Q = AL^{alpha} K^{beta} ]
Here, (A) represents total factor productivity, while (alpha) and (beta) measure the elasticity of output with respect to labor and capital. This model is particularly valuable because it reflects the realistic behavior of firms: as they increase one input while holding the other constant, the additional output generated gradually decreases.
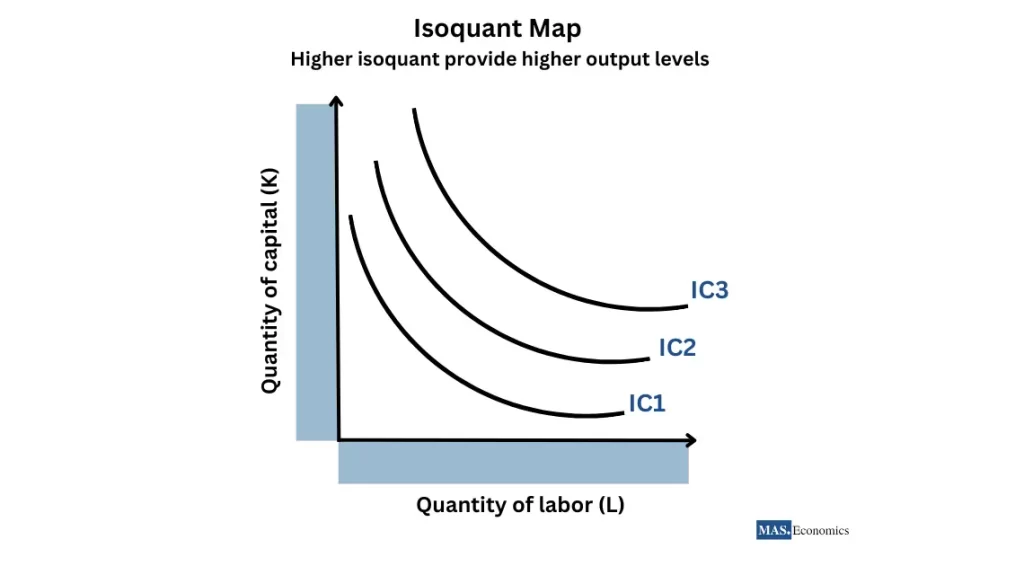
Isoquant Curves: Understanding Input Combinations
An isoquant curve shows all possible combinations of two inputs (labor and capital) that produce the same level of output. These curves enable firms to identify the most cost-effective input mix for their production needs.
Properties of Isoquant Curves
Isoquant curves exhibit several key properties:
Downward Sloping
An isoquant curve slopes downward, meaning that as a firm uses more of one input, it can reduce the other while maintaining the same output. This reflects the trade-off between labor and capital in production.
Convex to the Origin
Isoquant curves are convex to the origin due to diminishing marginal returns. As more of one input is used, its additional contribution to output decreases, and firms must use increasing amounts of the other input to maintain the same production level.
Higher Isoquants Represent Higher Output Levels
Isoquants further from the origin represent higher output levels. Firms moving to a higher isoquant must increase their inputs, signaling higher productivity.
Isoquants Do Not Intersect
Each isoquant represents a distinct output level. If two isoquants were to intersect, it would imply that the same input combination could produce two different output levels, which is impossible.
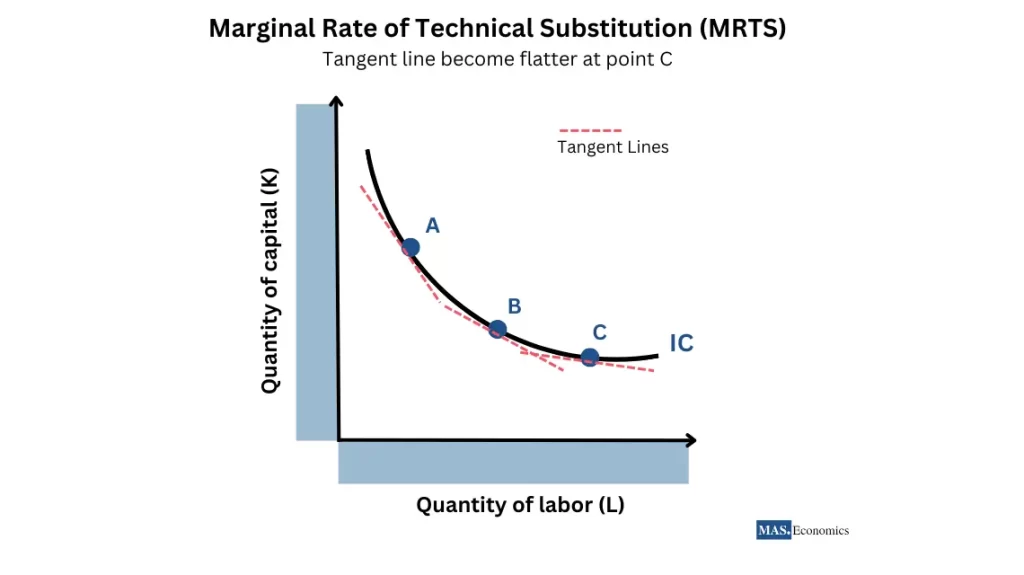
Marginal Rate of Technical Substitution (MRTS)
The Marginal Rate of Technical Substitution (MRTS) measures how much of one input a firm can give up while increasing the other input to keep output constant. MRTS is represented as the slope of the isoquant curve and is mathematically expressed as:
[ Q = AL^{alpha} K^{beta} ]
Here, (A) represents total factor productivity, while (alpha) and (beta) measure the elasticity of output with respect to labor and capital. This model is particularly valuable because it reflects the realistic behavior of firms: as they increase one input while holding the other constant, the additional output generated gradually decreases.
The Law of Production
The Law of Production describes how output responds to changes in input levels, focusing on two key principles: diminishing returns and returns to scale.
The Law of Diminishing Returns
This principle states that as more of a variable input (e.g., labor) is added to a fixed input (e.g., machinery), the additional output generated by the extra input will eventually decrease. Initially, adding more labor increases productivity, but after a certain point, the marginal returns begin to decline.
For example, in a factory with limited machinery, adding more workers may initially increase output, but overcrowding can eventually reduce productivity as workers compete for access to equipment.
Returns to Scale
Returns to scale refer to how output changes when all inputs increase proportionately. There are three types of returns to scale:
Increasing Returns to Scale
Output increases by a greater proportion than the increase in inputs. This often occurs due to economies of scale, such as bulk purchasing or specialization of labor.
Constant Returns to Scale
Output increases in the same proportion as inputs. This indicates that the firm is operating efficiently, and scaling production neither improves nor worsens productivity.
Decreasing Returns to Scale
Output increases by a smaller proportion than the increase in inputs. This can happen when firms become too large, leading to management inefficiencies and coordination problems.
Conclusion
Production functions and isoquant curves are essential tools for understanding how firms optimize input combinations to maximize output. The Cobb-Douglas function allows firms to model the relationship between labor, capital, and output while accounting for diminishing returns. Meanwhile, isoquant curves provide a graphical tool for visualizing different input combinations that achieve the same level of production, helping firms make informed decisions about resource allocation. By examining diminishing returns and returns to scale, firms can make informed decisions about scaling operations and managing resources efficiently.
FAQs:
What is a production function in economics?
A production function expresses the relationship between the inputs (such as labor and capital) used in production and the resulting output. It shows how much output a firm can produce given varying levels of input, helping businesses determine efficient resource allocation.
What are the main types of production functions?
- Linear Production Function: Output increases proportionally with inputs.
- Leontief Production Function: Inputs are used in fixed proportions; increasing one input alone will not raise output.
- Cobb-Douglas Production Function: Widely used, this function accounts for diminishing returns and varying input substitutability.
What is the Cobb-Douglas production function?
The Cobb-Douglas function takes the form
[ Q = AL^{alpha} K^{beta} ],
where (Q) is the output, (L) is labor, (K) is capital, (A) is total factor productivity, and (alpha) and (beta) represent the output elasticities of labor and capital. It reflects how changes in input levels impact output, considering diminishing returns.
What is the law of diminishing returns in production?
The law of diminishing returns states that as more units of a variable input (like labor) are added to a fixed input (like machinery), the additional output from each new unit of input will eventually decrease. For example, adding too many workers to a small workspace may reduce overall productivity.
What are returns to scale?
- Increasing Returns to Scale: Output increases by more than the proportional increase in inputs.
- Constant Returns to Scale: Output increases proportionally with inputs.
- Decreasing Returns to Scale: Output increases by less than the proportional increase in inputs.
What are isoquant curves?
Isoquant curves represent combinations of two inputs (like labor and capital) that yield the same level of output. These curves help firms identify efficient input combinations for production.
What are the properties of isoquant curves?
- Downward Sloping: As one input increases, the other can decrease to maintain the same output level.
- Convex to the Origin: Reflects diminishing marginal returns—more of one input is required to replace the other.
- Higher Isoquants Indicate Higher Output: Moving to a higher isoquant means more inputs are used, producing greater output.
- Isoquants Do Not Intersect: Each isoquant represents a unique output level, so they cannot overlap.
What is the Marginal Rate of Technical Substitution (MRTS)?
MRTS measures how much of one input a firm can give up while increasing the other to maintain the same output. It is the slope of the isoquant curve and reflects the trade-off between inputs like labor and capital.
How does MRTS change along an isoquant curve?
As a firm substitutes labor for capital along an isoquant curve, the MRTS decreases. This means that at higher levels of one input, each additional unit of that input becomes less effective at replacing the other.
What is the difference between the Cobb-Douglas and Leontief production functions?
- Cobb-Douglas Function: Allows for input substitutability and diminishing returns, making it more flexible.
- Leontief Function: Assumes inputs are used in fixed proportions, meaning that one input cannot replace another.
How do firms use isoquant curves in decision-making?
Firms use isoquant curves to determine the most efficient combination of inputs to produce a specific output. By comparing isoquants with cost lines (isocosts), firms can find the input mix that minimizes production costs.
Can you provide an example of the law of diminishing returns?
In a small factory with limited machinery, adding more workers may initially increase output. However, after a point, overcrowding reduces productivity, as workers compete for access to equipment—demonstrating diminishing returns.
What are economies of scale, and how do they relate to returns to scale?
Economies of scale occur when a firm experiences increasing returns to scale, meaning output grows faster than input usage. This often results from factors like bulk purchasing or labor specialization, leading to lower per-unit costs.
What are constant returns to scale?
Constant returns to scale occur when output increases in the same proportion as inputs. This indicates that the firm is operating efficiently, with no advantage or disadvantage to scaling production.
How do firms achieve optimal input combinations using isoquant curves?
By plotting isoquant curves (showing combinations of labor and capital) against isocost lines (showing total input costs), firms can identify the point where an isoquant curve is tangent to the isocost line. This point reflects the most cost-effective input combination for a given level of output.
How do production functions and isoquant curves help firms manage resources?
Production functions provide mathematical models for predicting how input changes affect output, while isoquant curves visually represent input trade-offs. Together, these tools guide firms in optimizing resource use, managing costs, and scaling production efficiently.
Thanks for reading! Share this with friends and spread the knowledge if you found it helpful.
Happy learning with MASEconomics








